Chinese Postman Problem, Eulerian and Hamiltonian Paths, and GIS

- Published on
Article Number: 24
Chinese Postman Problem, Eulerian and Hamiltonian Paths
Readers who come across this article either know what they are looking for or have arrived out of curiosity. Also, I would like to point out that this article was prepared without using any AI tools.
What is the Chinese Postman Problem?
The famous Chinese postman must travel through all the streets of a city to deliver the letters he carries. He is required to do this in the shortest and most cost-effective way possible. In response to this problem, a Chinese mathematician named Meigi Guan developed an algorithm in 1960. We thank him for his contributions.
Application Fields
The main goal of this problem is to plan routes that cover all the streets of a city. For some companies, the main requirement is to traverse the streets, while for a natural gas distribution company, it could be to navigate pipeline networks. Expanding further, water management authorities may use it to inspect canals and water distribution networks, while electricity distribution companies may use it to inspect power lines.
Today, some companies deploy small robots inside pipelines to detect leaks and potential issues. In places where GPS is not available, these robots determine their direction based on gravitational orientation and follow routes using this method.
From my personal experience, we have used this method for 360° street photography and detecting gas leaks in natural gas pipelines.
What Does This Graph Structure Look Like?
To perform such studies accurately, whether the lines are geometric or not, their intersection points must be defined as nodes, and each segment between nodes must be designated as an edge, with defined start and end nodes. This is an essential principle of navigation systems and forms the backbone of their functionality.
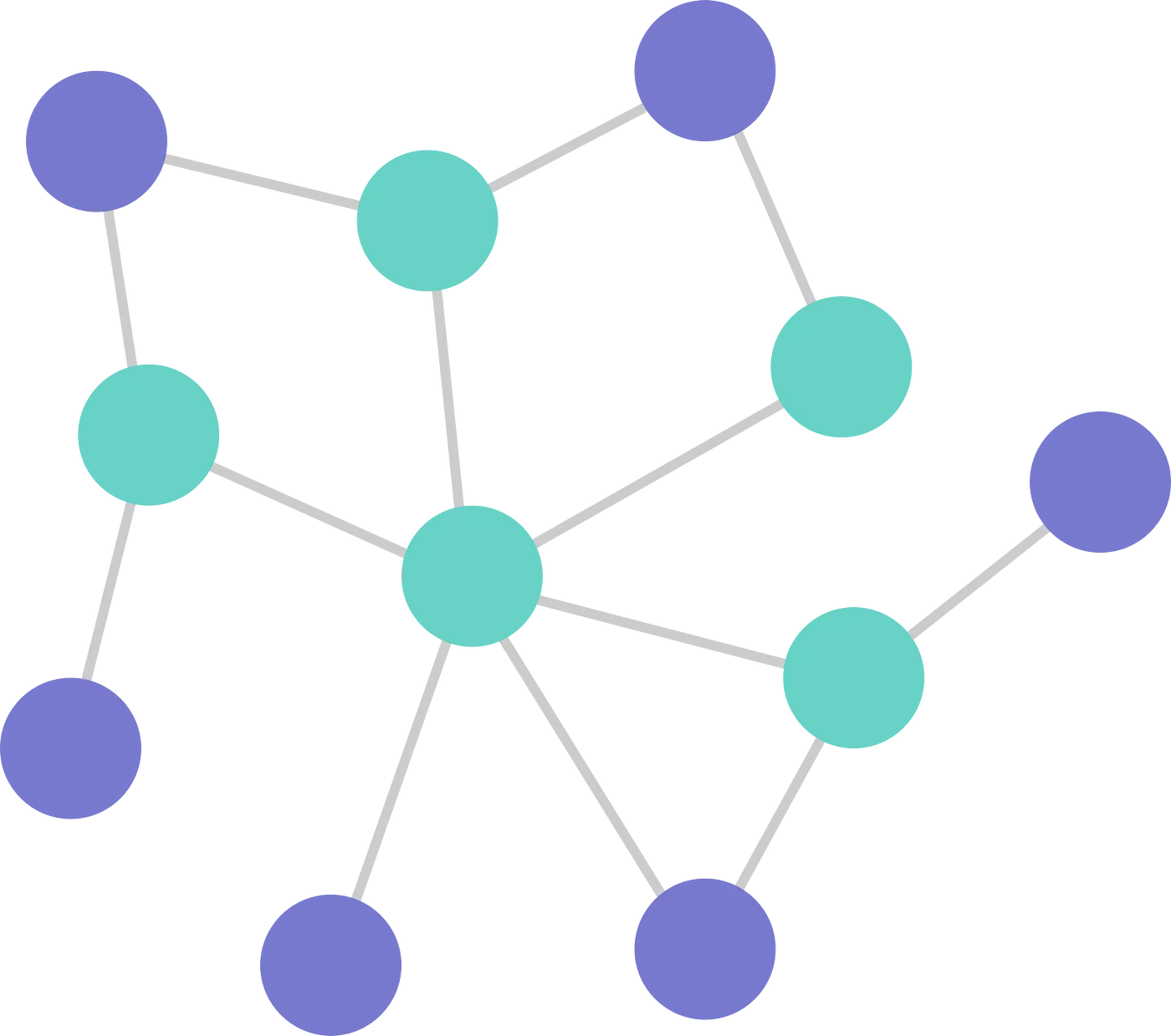
In the image above, the structure that defines the relationships between nodes and edges is called a graph.
Each blue and green dot in the image represents a node, while the connecting lines are referred to as edges.
The different colors in the image signify that while blue nodes serve as transition points between two nodes, green nodes connect to more than two points, similar to intersections or roundabouts in a city.
Eulerian Hatlar
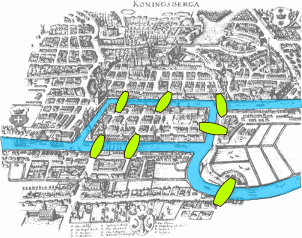
This problem was first discussed by Leonhard Euler in 1736 while solving the famous Seven Bridges of Königsberg problem.
As seen in the city on the left, there are seven bridges connecting four different land areas. The question posed was whether it was possible to traverse each bridge exactly once.
Although it seems like an abstract problem, it has significant real-world applications, such as determining garbage collection routes in cities. The goal is to ensure that every street is visited at least once.
Euler’s method ensures that at most two dead-end streets can exist, typically serving as the start and end points. Apart from these, all nodes must have an even number of edges. If a node has more than two odd-degree edges, it would be necessary to backtrack using an illegal method.
This method is the best approach for solving urban routing problems. However, some systems also use the Hamiltonian method.
Hamiltonian Paths
The key difference in this method is that every node in the graph must be visited at least once. That is, if a node is traversed more than once, the rule is violated. While the original problem was about a postman, remember that network analysis also includes applications for electricity, water, and natural gas distribution.
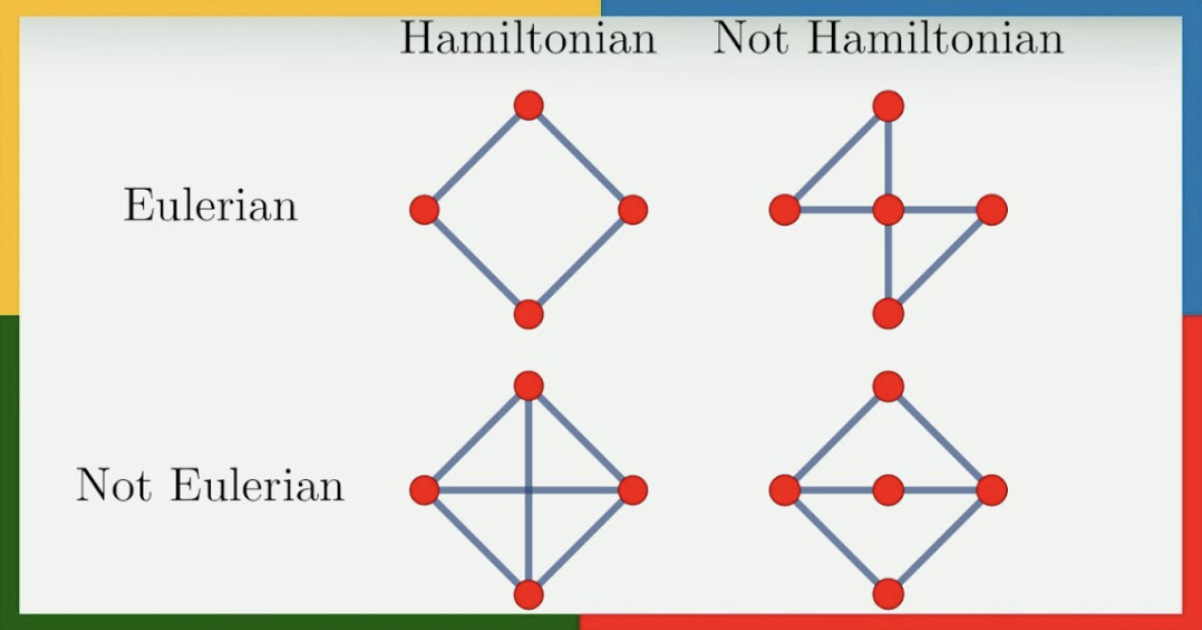
The image below shows an example where every node is visited at least once, demonstrating that both Eulerian and Hamiltonian methods should be chosen based on the needs of the problem.
What Are the Differences? Which One Should Be Used?
If you need to pass through every street in a city, Eulerian paths should be used. If you need to visit specific important points in the city, Hamiltonian paths are the better choice. Although these examples mainly focus on GIS, these methods are also widely used in electronics and other fields.

To better understand the differences, take another look at the examples below.
Eulerian Path vs. Hamiltonian Path Use Cases
| Application | Eulerian Path | Hamiltonian Path |
|---|---|---|
| Garbage collection | ✅ Evet | ❌ Hayır |
| Snow plowing | ✅ Evet | ❌ Hayır |
| Electricity/water distribution | ✅ Evet | ❌ Hayır |
| Navigation & delivery | ❌ Hayır | ✅ Evet |
| DNA sequencing | ❌ Hayır | ✅ Evet |
| Robotic systems | ❌ Hayır | ✅ Evet |
| Tourist route planning | ❌ Hayır | ✅ Evet |
Coding
If you want to get a quick result, I recommend using the Python programming language. Since there are many examples available online for Python, the example I will provide is prepared in JavaScript. Additionally, I want to explain the core concepts without using pre-built libraries, so you can understand the inner workings.
Creating a Graph Class
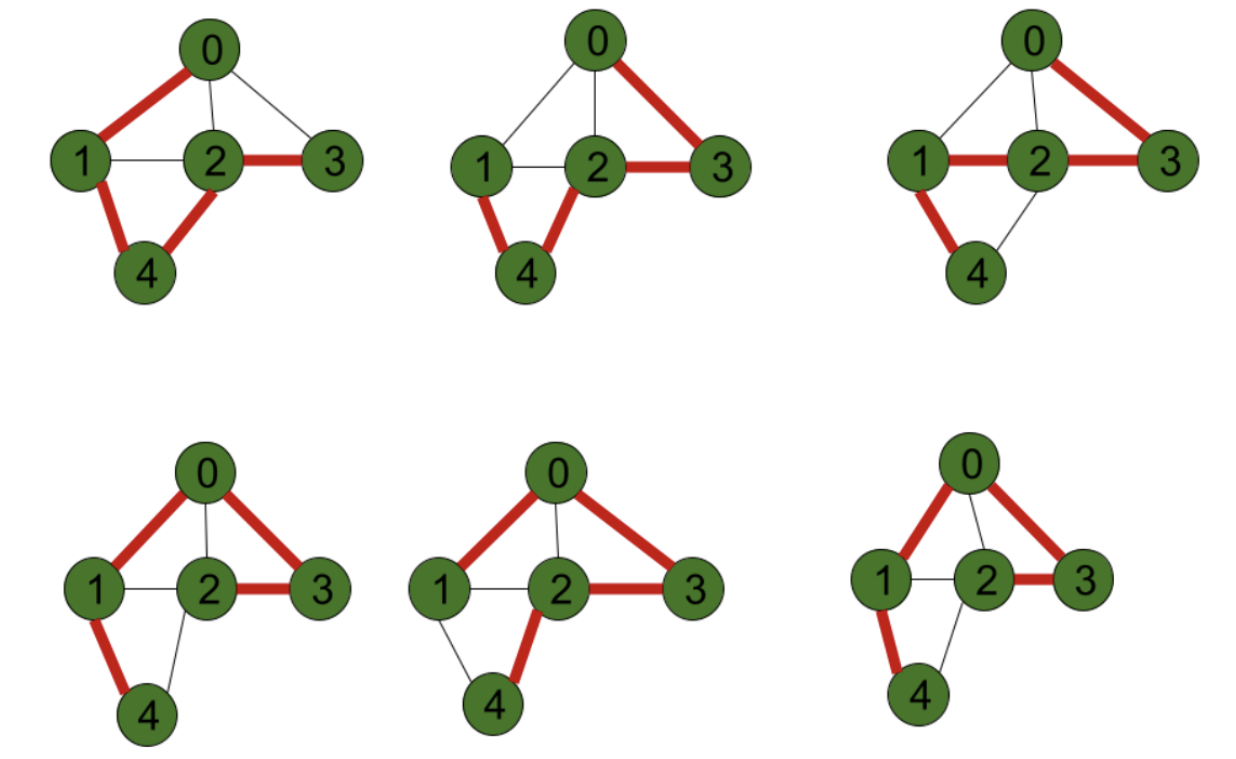
If we consider the graph on the left and assume that the edges are bidirectional, the possible paths are as follows:
1-0, 0-3, 3-4, 4-0, 0-2, 2-1, 1-2, 2-0, 0-4, 4-3, 3-0, 0-1.
Since each node has 2 edges, no matter where you start, you can always return to the starting node.
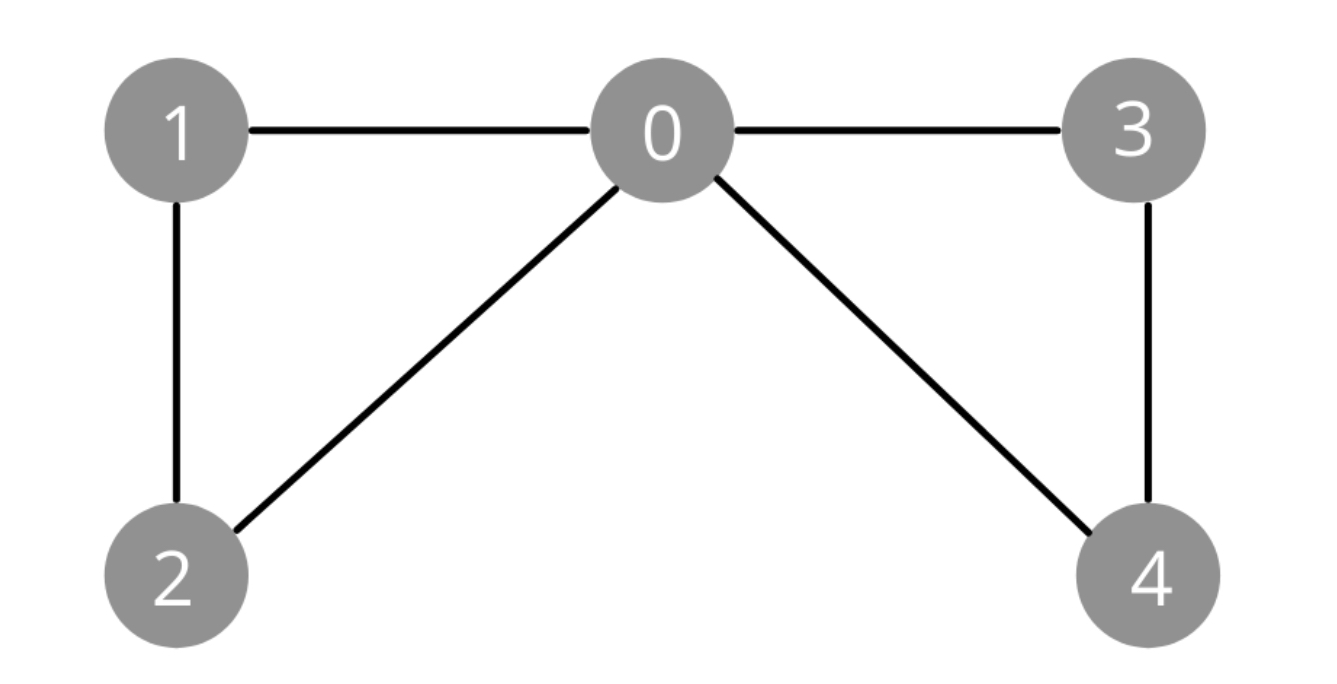
Now, let's define this in code. The following code is provided purely for understanding the logic, and you won’t need to use it later.
class Graph {
constructor() {
// Adjacency list to store the graph
this.adjacencyList = {};
}
// Function to add a node
addNode(node) {
if (!this.adjacencyList[node]) {
this.adjacencyList[node] = [];
}
}
// Function to add an edge (Undirected graph)
addEdge(node1, node2) {
if (this.adjacencyList[node1] && this.adjacencyList[node2]) {
this.adjacencyList[node1].push(node2);
this.adjacencyList[node2].push(node1); // Bidirectional connection
}
}
}
// Create a graph instance
const myGraph = new Graph();
// Add nodes
myGraph.addNode("0");
myGraph.addNode("1");
myGraph.addNode("2");
myGraph.addNode("3");
myGraph.addNode("4");
// Add edges (connections)
myGraph.addEdge("1", "0");
myGraph.addEdge("0", "3");
myGraph.addEdge("3", "4");
myGraph.addEdge("4", "0");
myGraph.addEdge("0", "2");
myGraph.addEdge("2", "1");
myGraph.addEdge("1", "2");
myGraph.addEdge("2", "0");
myGraph.addEdge("0", "4");
myGraph.addEdge("4", "3");
myGraph.addEdge("3", "0");
myGraph.addEdge("0", "1");
Once you have built your graph structure as shown in the example above, you can implement various algorithms on it.
Using graphlib.js
In practice, you would use the graphlib npm package, which simplifies graph handling. You will likely add nodes and edges in a loop, but the general idea is as follows:
import { Graph } from "graphlib";
// Create an undirected graph
const graph = new Graph({ directed: false });
// 📌 **Add nodes**
graph.setNode("A");
graph.setNode("B");
graph.setNode("C");
graph.setNode("D");
// 📌 **Add edges**
graph.setEdge("A", "B"); // A → B connection
graph.setEdge("A", "C"); // A → C connection
graph.setEdge("B", "D"); // B → D connection
graph.setEdge("C", "D"); // C → D connection
// 📌 **Print the graph**
console.log("Nodes:", graph.nodes()); // ["A", "B", "C", "D"]
console.log("Edges:", graph.edges()); // [{ v: "A", w: "B" }, { v: "A", w: "C" }, { v: "B", w: "D" }, { v: "C", w: "D" }]
Checking if a Graph is Eulerian
Once you have built your graph, you can use this method to check if it has an Eulerian path. The method returns true if the graph is Eulerian, otherwise false. If your project requires an Eulerian graph, you may need to add additional edges or mark some as bidirectional.
/**
* Checks if a graph has an Eulerian path.
* A graph contains an Eulerian path if it has at most 2 nodes with an odd degree.
*
* @param {Graph} g - A Graphlib instance (directed or undirected)
* @returns {boolean} - Returns true if an Eulerian path exists, otherwise false.
*/
function hasEulerianPath(g) {
let oddCount = 0; // Count of odd-degree nodes
g.nodes().forEach(n => {
// Calculate node's degree
const deg = (g.outEdges(n)?.length || 0) + (g.inEdges(n)?.length || 0);
if (deg % 2 !== 0) {
oddCount++; // Increment if degree is odd
}
});
// Eulerian path exists if there are 0 or 2 odd-degree nodes
return oddCount === 0 || oddCount === 2;
}
Finding an Eulerian Path
If your graph is Eulerian, you can use the following algorithm to find the Eulerian path. This function also utilizes the previous method to check if a path exists.
/**
* Finds the Eulerian path using Hierholzer's algorithm.
*
* @param {Graph} g - A Graphlib instance (directed or undirected)
* @returns {string[]} - Returns an array representing the Eulerian path.
*/
function findEulerianPath(g) {
if (!hasEulerianPath(g)) {
throw new Error('The graph does not have an Eulerian path.');
}
const edges = [...g.edges()];
const stack = [];
const path = [];
const adj = {};
// Build adjacency list
edges.forEach(({ v, w }) => {
if (!adj[v]) adj[v] = [];
adj[v].push(w);
});
let curr = edges[0].v;
stack.push(curr);
// Hierholzer's algorithm
while (stack.length > 0) {
if (adj[curr] && adj[curr].length > 0) {
stack.push(curr);
curr = adj[curr].pop(); // Move to next node
} else {
path.push(curr); // Backtrack
curr = stack.pop();
}
}
return path.reverse(); // Return reversed path
}
Finding a Hamiltonian Path
If your system requires every node to be visited exactly once (Hamiltonian path), use the following algorithm:
/**
* Finds a Hamiltonian path in a graph.
* A Hamiltonian path visits each node exactly once.
*
* @param {Graph} g - A Graphlib instance (directed or undirected)
* @returns {string[] | null} - Returns the Hamiltonian path as an array, or null if no path exists.
*/
function findHamiltonianPath(g) {
const nodes = g.nodes();
for (const start of nodes) {
const path = [start];
if (dfs(start, new Set([start]), path, g)) {
return path;
}
}
return null;
}
/**
* Depth-first search (DFS) with backtracking to find a Hamiltonian path.
*
* @param {string} node - The current node
* @param {Set<string>} visited - A set tracking visited nodes
* @param {string[]} path - The current path
* @param {Graph} g - The Graphlib graph
* @returns {boolean} - Returns true if a Hamiltonian path is found, otherwise false.
*/
function dfs(node, visited, path, g) {
if (visited.size === g.nodeCount()) return true;
for (const neighbor of g.successors(node) || []) {
if (!visited.has(neighbor)) {
visited.add(neighbor);
path.push(neighbor);
if (dfs(neighbor, visited, path, g)) return true;
// Backtracking
visited.delete(neighbor);
path.pop();
}
}
return false;
}
These codes were prepared with comments to help you understand how they work. Now, you can combine them as you wish. My recommendation is to create your own class. You can structure it as follows and fill in the methods according to your needs.
Finall Code - GL class
import { Graph } from "graphlib";
class GL {
constructor(nodes, edges) {
this.graph = new Graph({ directed: true });
// Add nodes
nodes.forEach(n => this.graph.setNode(n));
// Add edges
edges.forEach(({ from, to }) => this.graph.setEdge(from, to));
}
/**
* Checks if the graph has an Eulerian path.
* @returns {boolean}
*/
static hasEulerianPath(g) {
let oddCount = 0;
g.nodes().forEach(n => {
const deg = (g.outEdges(n)?.length || 0) + (g.inEdges(n)?.length || 0);
if (deg % 2 !== 0) oddCount++;
});
return oddCount === 0 || oddCount === 2;
}
/**
* Finds the Eulerian path using Hierholzer's Algorithm.
* @returns {string[]} - The Eulerian path or an error
*/
static findEulerianPath(g) {
if (!this.hasEulerianPath(g)) {
throw new Error('The graph does not have an Eulerian path.');
}
const edges = [...g.edges()];
const stack = [], path = [];
const adj = {};
// Create adjacency list
edges.forEach(({ v, w }) => {
if (!adj[v]) adj[v] = [];
adj[v].push(w);
});
let curr = edges[0].v;
stack.push(curr);
while (stack.length > 0) {
if (adj[curr] && adj[curr].length > 0) {
stack.push(curr);
curr = adj[curr].pop();
} else {
path.push(curr);
curr = stack.pop();
}
}
return path.reverse();
}
/**
* Finds the Hamiltonian path.
* @returns {string[] | null} - The Hamiltonian path or null
*/
static findHamiltonianPath(g) {
const nodes = g.nodes();
for (const start of nodes) {
const path = [start];
if (this.dfs(start, new Set([start]), path, g)) {
return path;
}
}
return null;
}
/**
* DFS algorithm for finding a Hamiltonian path (using backtracking).
* @returns {boolean}
*/
static dfs(node, visited, path, g) {
if (visited.size === g.nodeCount()) return true;
for (const neighbor of g.successors(node) || []) {
if (!visited.has(neighbor)) {
visited.add(neighbor);
path.push(neighbor);
if (this.dfs(neighbor, visited, path, g)) return true;
visited.delete(neighbor);
path.pop();
}
}
return false;
}
/**
* Returns either the Eulerian or Hamiltonian path.
* @param {"eulerian" | "hamiltonian"} type - Type of path to find
* @returns {string[] | null} - The found path or null
*/
getPath(type) {
if (type === "eulerian") {
return GL.findEulerianPath(this.graph);
} else if (type === "hamiltonian") {
return GL.findHamiltonianPath(this.graph);
}
return null;
}
}
// Example Usage:
const nodes = ["A", "B", "C", "D"];
const edges = [{ from: "A", to: "B" }, { from: "B", to: "C" }, { from: "C", to: "D" }, { from: "D", to: "A" }];
const graph = new GL(nodes, edges);
console.log("Eulerian Path:", graph.getPath("eulerian"));
console.log("Hamiltonian Path:", graph.getPath("hamiltonian"));
If you have any questions please write me.