Makale Numarasi : 24

Çinli Postacı Problemi, Eulerian ve Hamiltonian Hatlar

Bu yazıyı okumaya gelen kişiler ne aradıklarını bilerek ya da merak ettikleri için gelmiş olacaklar. Ayrıca bilmenizi isterim ki bu yazı herhangi bir yapay zeka aracı kullanılmadan hazırlanmıştır.

Çinli Postacı Problemi Nedir ?

Bahsi geçen meşhur Çinli postacımız elinde var olan mektupları dağıtmak için şehrin tüm sokaklarından geçmesi gerekmiştir ve bunu en kısa yoldan en az maliyetle yapmasını isterler. Bunun üzerine Meigi Guan adlı bir Çinli matematikçi 1960 yılında bir algoritma geliştirir. Katkılarından dolayı teşekkür ederiz.

Kullanım Yerleri

Problemimiz bir şehrin tüm sokaklarını gezebileceğimiz rotaları planlanlamaktır. Buna göre bazı şirketlerin asıl ihtiyacı sokakların gezilmesi olurken, bir doğalgaz dağıtım şirketi için doğalgaz boru hatlarını dolaşmak olacaktır. Biraz daha çeşitlendirecek olursak su idareleri kanal ve su şebekeleri kontrolü için kullanırken elektrik dağıtım şirketleri ise enerji nakil hatlarını kontrol için kullanmak isteyecektir.

Öyle ki günümüzde bazı şirketler boru hatlarının içerisine minik robotlar göndererek olası kaçakları ve sorunları bulmaya çalışıyor. GPS in mümkün olmadığı yerlerde yer çekimi yönüne göre hareketlerinin yönünü belirleyen robotlar hatlar içerisinde gezerken elbette bu yöntemi kullanarak yoluna devam edeceklerdir.

Benim kişisel olarak içerisinde bulunduğum projelerden örnek verecek olursam; 360° derece sokak fotoğrafı çekimleri ve doğalgaz borularında oluşan kaçak gaz tespiti işleminde kullandık.

Bu Graf Yapı Neye Benziyor?

Tabii ki böyle çalışmaları doğru bir şekilde yapabilmek için hatlarınız ister geometrik olsun ya da olmasın birbirleri ile kesiştikleri noktaların node olarak tanımlanması ve nodelar arasında kalan her hattın edge olarak başlangıç ve bitiş node ile ilişkilendirilmiş olması gerekmektedir. Bu, navigasyon sistemlerinin vazgeçilmek kuralı olup sistemin çalışmasını sağlayan temel unsurdur.

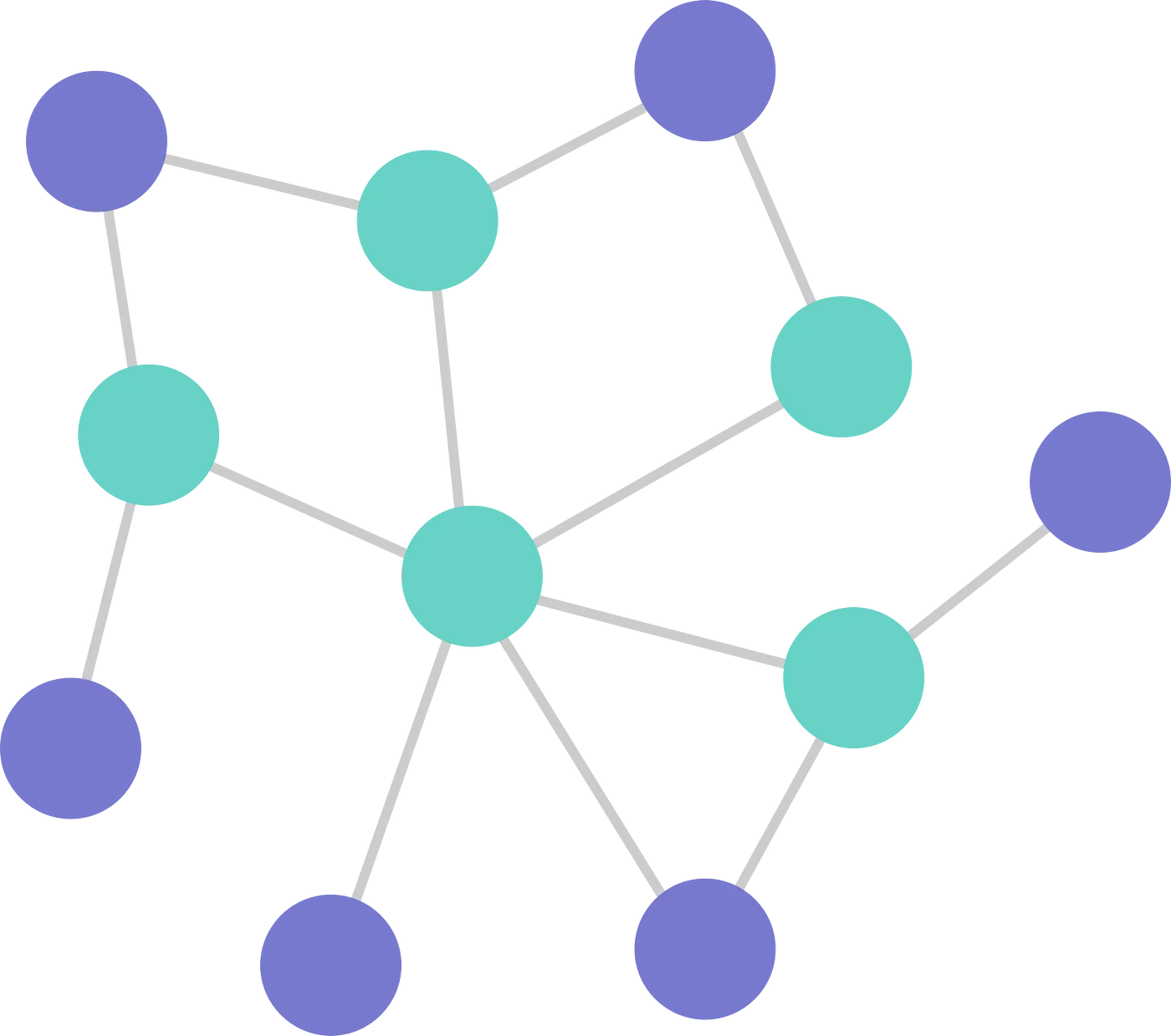
Yukarıda yer alan resimde node ve edgelerin ilişkilerini bir arada tanımlayan yapılara graf adı verilmektedir.

Bu görselde olduğu gibi mavi ve yeşil noktaların her biri node noktalarıdır ve arada kalan hatlar ise edge olarak isimlendirilmektedir.

Görselde renklerinin farklı olmasının sebebi mavilerin iki node arasında bir geçiş noktası olurken yeşillerin farkı ise rota oluşurken ikiden fazla noktaya ulaştırabilmesidir. Yani şehrinizde yer alan kavşak ve dört yol gibi noktalara benzetilebilirsiniz.

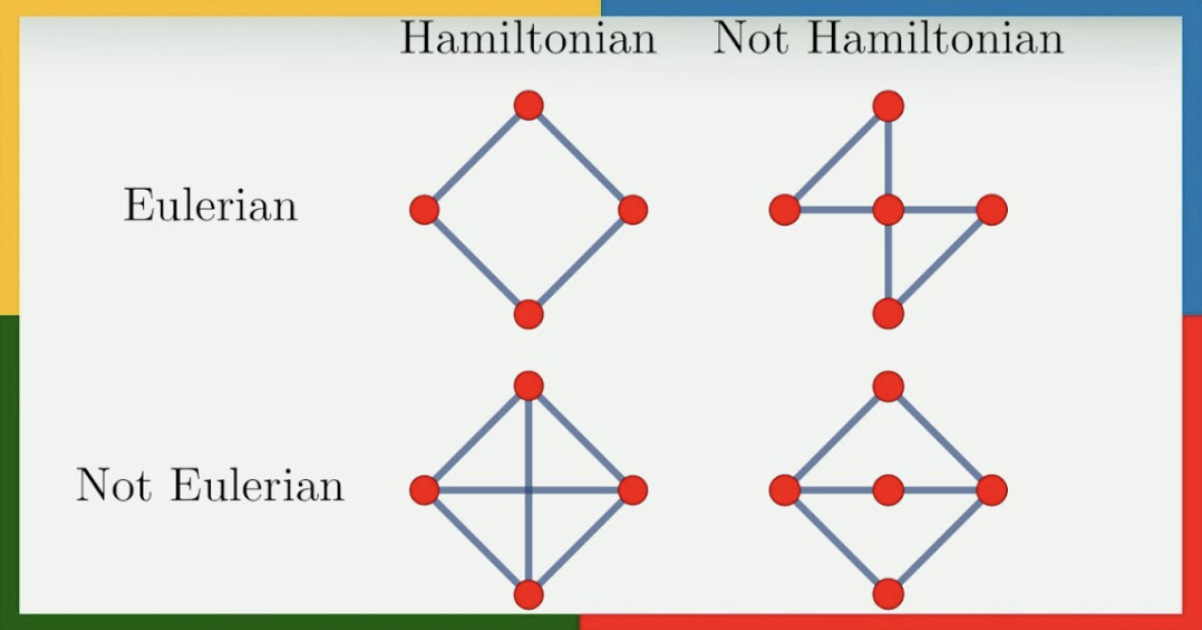
Eulerian Hatlar

Bu problem ilk olarak Leonhard Euler tarafından 1736'da ünlü Königsberg'in Yedi Köprüsü problemini çözerken tartışma konusu olmuştur. Solda gördüğünüz şehirde yedi farklı köprü vardır ve geçişler dört farklı parçadan oluşan bu şehri birbirine bağlayan bu köprüler üzerinden yapılmaktadır. Bu nedenle her köprüden en az bir kez geçecek şekilde tüm köprülerden geçilebilir mi konusu ortaya atılması üzerine çözüm için söz konusu olmuştur.

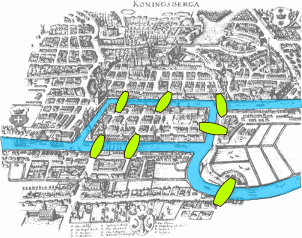
Görünüşe göre şehirlerin kurulmasında görünmeyen ancak önemli bir rolü olan bir konu bu. Böylece sokağımızda bulunan çöp toplama araçları çok kez bu yönteme başvurur. Burada amaç güzergah içerisinde her sokağa en az bir kez uğrayabilmektir. Eulerin konusu en fazla bu sokaktan geçmek olsa da çift yönlü yolların var olması çıkmaz sokaklardan kurtulmak adına önemli olacaktır.

Euler yöntemini kullanarak tüm yollara uğranan sistemlerde en falza iki çıkmaz yol olabilir. Bu da genelde başlangıç ve bitiş yollarının olabilmesi içindir. Bunun dışında kalan tüm node lara bağlı edge sayısı mutlaka çift olmalıdır. Öyle ki eğer sistemde ikiden fazla tek sayılı edgeye sahip olan node varsa mecburen illegal bir yöntemle yoldan geri dönmek gerekecektir. Bu nedenle ben sistemimi eulerian yapmam gerektiğinde mecburen sorun yaratan sokağı çift şeritliymiş gibi gösteriyorum.

Şehir içi yollarda sonuç üretmek için kullanılabilen en iyi yöntemdir. Ancak Hamilton yöntemini kullanan sistemler de var.

Hamiltonian Hatlar

Bu yöntemin farkı ise uğranması gereken tüm node noktaları graph içerisinde en az bir kez uğranması gerekmektedir. Yani bir node üzerinden ikinci kez geçilirse bu kuralı ihlal etmektedir. Konumuzun çıkış noktası postacıydı ancak unutmamak gerekir ki network analiz kapsamında elektrik su ve doğalgaz hatları da var.

Aşağıda yer alan resimde bir graf içerisinde herhangi bir noktadan başladığında her noktaya uğrayacağınız bir örnek gösterilmiştir. Bu demek oluyor ki Euler yöntemi de Hamilton yöntemi de ihtiyaca göre tercih edilmelidir.

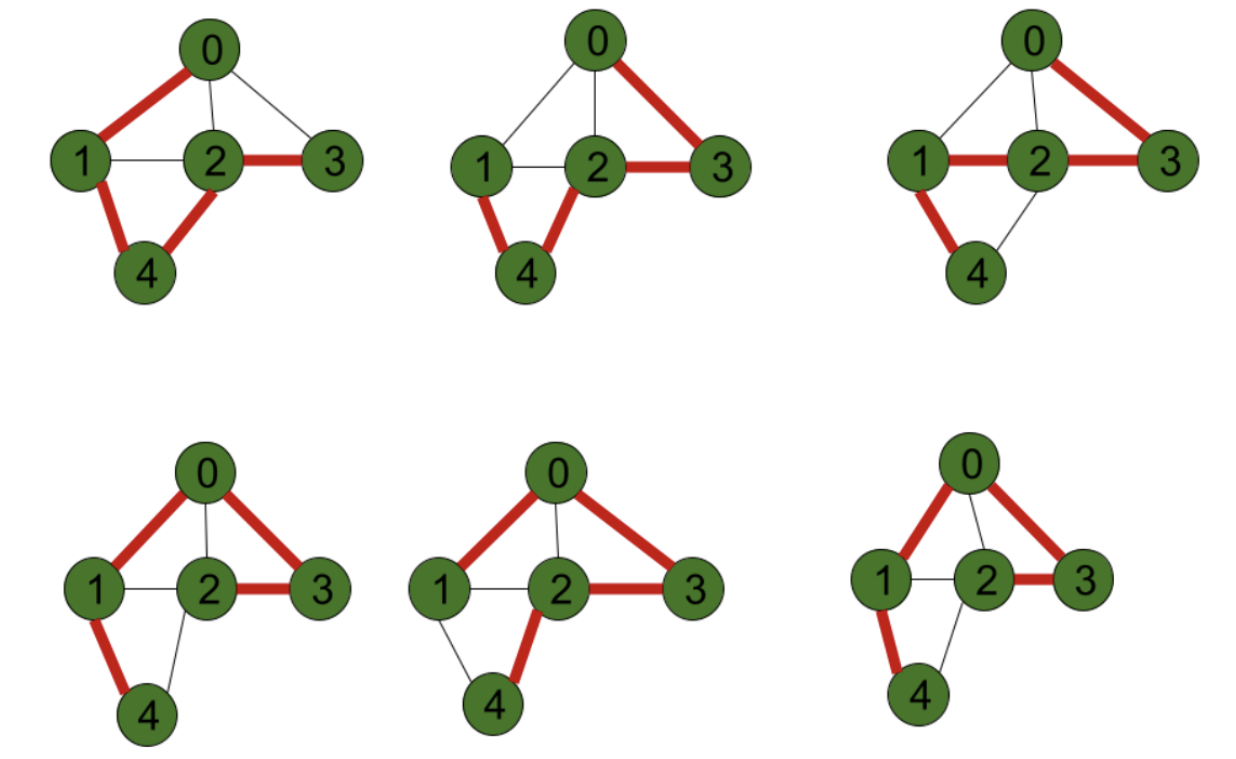
Farkları Nedir Hangisini Kullanmalıyız ?

Eğer şehrin her sokağından geçmeniz gerekiyorsa Euler, şehirde önemli noktalara uğrayacaksanız Hamilton yöntemini tercih etmeniz gerekecektir. Bu örneklerimiz genelde GIS üzerine olsa da elektronik sektöründe de kullanılan yöntemlerdir. Aradaki farkı biraz daha ortaya çıkarmak için aşağıdaki örnekleri tekrar bir gözden geçirmekte fayda var.

Bazı kullanım farklılıkları aşağıdaki tabloda gösterilmektedir. Çöp toplama sürecinin her sokakta olduğu farz edilerek hazırlanmıştır.

Eulerian Yol vs Hamiltonian Yol Kullanım Alanları

Günlük Kullanım	Eulerian Hat	Hamiltonian
Çöp toplama	✅ Evet	❌ Hayır
Kar küreme	✅ Evet	❌ Hayır
Elektrik-su hatları	✅ Evet	❌ Hayır
Navigasyon ve kargo	❌ Hayır	✅ Evet
DNA dizileme	❌ Hayır	✅ Evet
Robotik sistemler	❌ Hayır	✅ Evet
Turistik gezi planı	❌ Hayır	✅ Evet

Kodlaması

Hızlı bir sonuç üretmek istiyorsanız eğer python dilini kullanmanızı öneriyorum. İnternette python ile çok fazla örnek olması sebebi ile benim vereceğim örnek javascript için hazırlanmıştır. Hatta işin mutfağını anlamanız için hazır kütüphaneler kullanmadan anlatmak istiyorum.

Graph Class'ın Oluşturulması

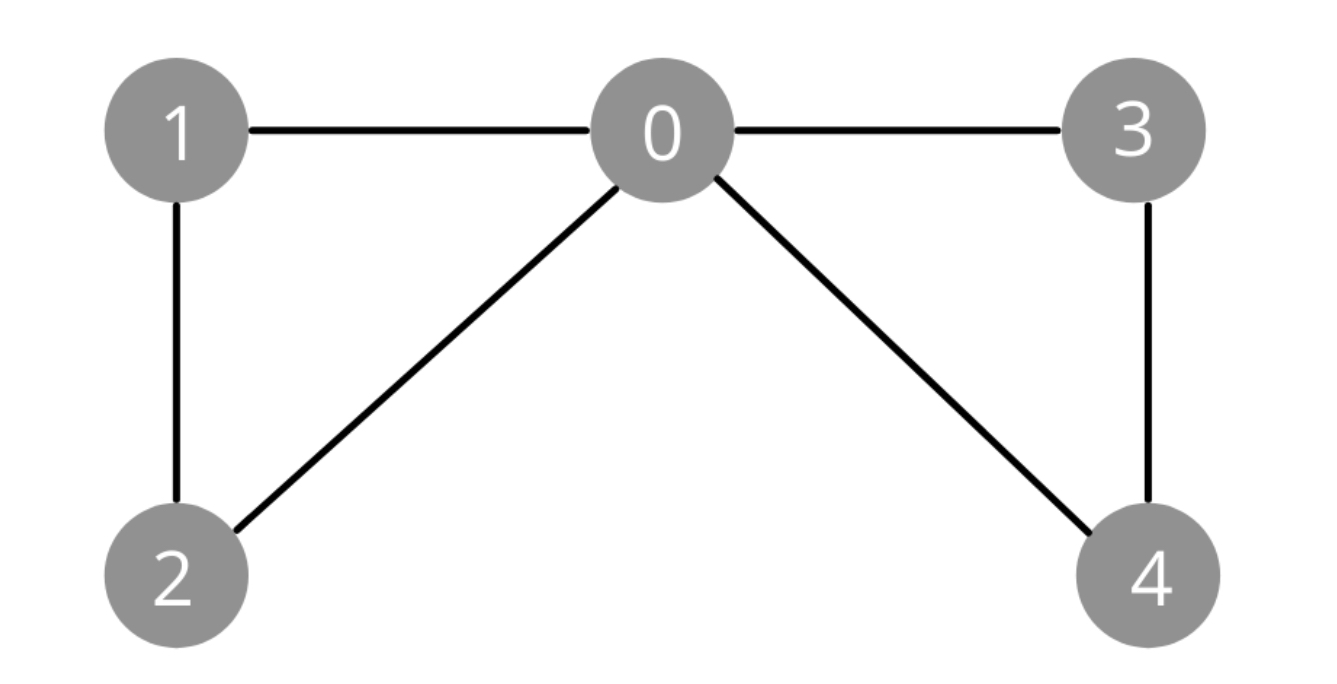
Solda görünen grafda edge hatlarının çift şeritli olduğunu düşünerek hareket edecek olursak eğer gidilebilecek yol olasılıkları

1-0, 0-3, 3-4, 4-0, 0-2, 2-1, 1-2, 2-0, 0-4, 4-3, 3-0, 0-1 gibi gidiş geliş yolları vardır. Her node 2 edge’e sahip olması nedeniyle hani noktadan başlarsanız başlayın ilk noktanıza tekrar ulaşabileceğiniz anlamına da gelmektedir.

O halde bunu kod tarafında tanımlayalım. Aşağıdaki kodu daha sonra kullanmayacaksınız. Sadece mantığını anlamanız amaçlanmıştır.

class Graph {
  constructor() {
    // Komşuluk listesi (grafı saklamak için obje)
    this.adjacencyList = {}; 
  }
  // Düğüm ekleme fonksiyonu
  addNode(node) {
    if (!this.adjacencyList[node]) {
      this.adjacencyList[node] = [];
    }
  }
  // Kenar (bağlantı) ekleme fonksiyonu (Yönsüz graf)
  addEdge(node1, node2) {
    if (this.adjacencyList[node1] && this.adjacencyList[node2]) {
      this.adjacencyList[node1].push(node2);
      this.adjacencyList[node2].push(node1); // Yönsüz olduğu için çift taraflı bağlantı
    }
  }
}
// Graf Nesnesini oluşturma
const myGraph = new Graph();
// Düğümleri ekleyelim
myGraph.addNode("0");
myGraph.addNode("1");
myGraph.addNode("2");
myGraph.addNode("3");
myGraph.addNode("4");
// Kenarları (bağlantıları) ekleyelim
myGraph.addEdge("1", "0");
myGraph.addEdge("0", "3");
myGraph.addEdge("3", "4");
myGraph.addEdge("4", "0");
myGraph.addEdge("0", "2");
myGraph.addEdge("2", "1");
myGraph.addEdge("1", "2");
myGraph.addEdge("2", "0");
myGraph.addEdge("0", "4");
myGraph.addEdge("4", "3");
myGraph.addEdge("3", "0");
myGraph.addEdge("0", "1");

Graph mantığını anlamanız için hazırladığım yukarıdaki kodda Bu şekilde graph yapınızı oluşturduktan sonra artık çeşitli algoritmalarınızı çalıştırabilirsiniz. Peki biz normalde nasıl kullanırız? graphlib adında bir npm paketi bulunmaktadır. Oldukça basit yapıda olan bu paket zaten sizin yazacağınız graph kodunu hazır bir şekilde kullanmanıza yardımcı olacaktır.

graphlib ile yazacağınız zaman elinizdeki node ve edgeleri muhtemelen bir döngü içerisinde ekleyeceksiniz ancak genel mantığı aşağıdaki gibidir.

import { Graph } from "graphlib";

// Yönsüz (undirected) bir grafik oluştur
const graph = new Graph({ directed: false });

// 📌 **Düğümler ekleyelim**
graph.setNode("A");
graph.setNode("B");
graph.setNode("C");
graph.setNode("D");

// 📌 **Kenarlar ekleyelim**
graph.setEdge("A", "B"); // A → B bağlantısı
graph.setEdge("A", "C"); // A → C bağlantısı
graph.setEdge("B", "D"); // B → D bağlantısı
graph.setEdge("C", "D"); // C → D bağlantısı

// 📌 **Grafı yazdıralım**
console.log("Nodes:", graph.nodes());   // ["A", "B", "C", "D"]
console.log("Edges:", graph.edges());   // [{ v: "A", w: "B" }, { v: "A", w: "C" }, { v: "B", w: "D" }, { v: "C", w: "D" }]

Bir Graphın Eulerian durumunu kontrol etme Algoritması

Oluşturacağınız graph'ı sonrasında bu metodu kullanırken parametre olarak vereceksiniz. Bu metodun geri dönüş değeri boolean olarak true ya da false olacaktır. Eğer true ise Euleriandır ama eğer false ise Eulerıan değildir. Eğer projenizdin Eulerian olmasını istiyorsanız ya yeni bir ara hat eklemeniz gerekir ya da bazı hatları mecburi olarak çift yönlü yapılması gerekecektir.

/**
 * Grafın Eulerian yolu olup olmadığını kontrol eder.
 * Bir graf Eulerian yol içeriyorsa, en fazla 2 tane tek dereceli düğüme sahip olmalıdır.
 * 
 * @param {Graph} g - Graphlib nesnesi (yönlü veya yönsüz grafik)
 * @returns {boolean} - Eulerian yol varsa true, yoksa false döner
 */
function hasEulerianPath(g) {
    // Tek dereceli düğüm sayısı
    let oddCount = 0; 

    g.nodes().forEach(n => {
      // Düğümün çıkış ve giriş derecelerini hesapla
      const deg = (g.outEdges(n)?.length || 0) + (g.inEdges(n)?.length || 0);
      if (deg % 2 !== 0) {
        // Eğer derece tekse, sayacı artır
        oddCount++; 
      }
    });

    // Eulerian yol için tek dereceli düğüm sayısı 0 veya 2 olmalıdır
    return oddCount === 0 || oddCount === 2;
}

Bir Graph'da Eulerian Path'i Bulmak

Bu da artık bu adımın sonuç ürünlerinden birisi artık Eulerian. olan hattınızı bu algoritma ile kolayca bulabilirsiniz. Ayrıca bu algorıtma bir üstte yer alan ve Graphın Eulerian olup olmamasını kontrol eden kodu da kullanmaktadır.

/**
 * Eulerian yolunu bulan algoritma (Hierholzer Algoritması kullanır).
 * Grafın Eulerian yolu olup olmadığı kontrol edilir, ardından yolu oluşturur.
 * 
 * @param {Graph} g - Graphlib nesnesi (yönlü veya yönsüz grafik)
 * @returns {string[]} - Eulerian yolunu içeren düğüm sırası
 */
function findEulerianPath(g) {
    if (!hasEulerianPath(g)) {
        throw new Error('The graph does not have an Eulerian path.');
    }

    const edges = [...g.edges()]; // Grafın kenarlarını al
    const stack = []; // DFS için yığın
    const path = []; // Eulerian yolu
    const adj = {}; // Komşuluk listesi (adjacency list)

    // Komşuluk listesini oluştur
    edges.forEach(({ v, w }) => {
        if (!adj[v]) adj[v] = [];
        adj[v].push(w);
    });

    // İlk düğümü belirle ve yığına ekle
    let curr = edges[0].v;
    stack.push(curr);

    // DFS ile Eulerian yolu oluştur
    while (stack.length > 0) {
        if (adj[curr] && adj[curr].length > 0) {
            stack.push(curr);
            curr = adj[curr].pop(); // Bir sonraki düğüme git
        } else {
            path.push(curr); // Çıkmaz noktaya ulaşıldıysa yola ekle
            curr = stack.pop(); // Geri dön
        }
    }

    return path.reverse(); // Yol ters çevrilerek döndürülür
}

Sonuç olarak günümüzde sokaklar için çalışıyorsanız kullanmanız gereken algoritmada hatların eulerian olmasını bekleyebilirsiniz. Eğer her node dan bir kez geçilmek zorunda ise yani bu onun Hamiltonian olması gerektiği anlamına gelir bunun algoritması da aşağıdaki gibi olacaktır.

Hamiltonian Path'i bulmak

Aşağıda ki kod bloğunda ise graph içerisindeki her node noktasına en az bir kere uğramanız için gereken Hamiltonian path bulma algoritmasını ekledim. Bu pathler size en son olarak string array dönecekler ve bu array içerisinde node numaraları olacak. Bu noktadan sonra bu sıralamaya denk gelen nod noktalarının geometrik bilgileri zaten sizde var. İstediğiniz şekilde yönetebilirsiniz. Ben LineString bir geojson oluşturmak için kullanıyorum.

/**
 * Bir graf içinde Hamiltonian yol olup olmadığını bulan algoritma.
 * Hamiltonian yol, her düğümü yalnızca bir kez ziyaret eden bir yoldur.
 *
 * @param {Graph} g - Graphlib nesnesi (yönlü veya yönsüz grafik)
 * @returns {string[] | null} - Hamiltonian yolu içeren düğüm sırası veya null (bulunamazsa)
 */
function findHamiltonianPath(g) {
    const nodes = g.nodes(); // Grafın düğümlerini al

    // Her düğümü başlangıç düğümü olarak dene
    for (const start of nodes) {
        const path = [start]; // Yol dizisini başlat
        if (dfs(start, new Set([start]), path, g)) {
            return path; // Hamiltonian yol bulundu
        }
    }

    return null; // Hamiltonian yol bulunamazsa null döndür
}

/**
 * Derinlik Öncelikli Arama (DFS) ile Hamiltonian yol araması yapar.
 *
 * @param {string} node - Şu anki düğüm
 * @param {Set<string>} visited - Ziyaret edilen düğümleri takip eden küme
 * @param {string[]} path - Geçerli yolu saklayan dizi
 * @param {Graph} g - Graphlib grafı
 * @returns {boolean} - Eğer Hamiltonian yol bulunduysa true, aksi halde false
 */
function dfs(node, visited, path, g) {
    if (visited.size === g.nodeCount()) {
        return true; // Tüm düğümler ziyaret edildi, yol bulundu
    }

    // Mevcut düğümün komşularını kontrol et
    for (const neighbor of g.successors(node) || []) {
        if (!visited.has(neighbor)) {
            visited.add(neighbor);
            path.push(neighbor);

            if (dfs(neighbor, visited, path, g)) {
                return true; // Yol bulunduysa geriye true döndür
            }

            // Geri dönüş (backtracking)
            visited.delete(neighbor);
            path.pop();
        }
    }

    return false; // Yol bulunamazsa false döndür
}

Bu kodlar nasıl kullanıldığınız anlamanız için açıklama satırları ile hazırlanmış halleriydi. Şimdi dilediğiniz gibi birleştirebilirsiniz. Benim size önerim kendinize ait bir class oluşturmanızdır. Genel yapıyı şu şekilde oluşturabilir metodların içerisini kendinize göre doldurabilirsiniz.

Sonuç Ürünü - GL class

import { Graph } from "graphlib";

class GL {
    constructor(nodes, edges) {
        this.graph = new Graph({ directed: true });

        // Düğümleri ekle
        nodes.forEach(n => this.graph.setNode(n));

        // Kenarları ekle
        edges.forEach(({ from, to }) => this.graph.setEdge(from, to));
    }

    /**
     * Grafın Eulerian yolu olup olmadığını kontrol eder.
     * @returns {boolean}
     */
    static hasEulerianPath(g) {
        let oddCount = 0;

        g.nodes().forEach(n => {
            const deg = (g.outEdges(n)?.length || 0) + (g.inEdges(n)?.length || 0);
            if (deg % 2 !== 0) oddCount++;
        });

        return oddCount === 0 || oddCount === 2;
    }

    /**
     * Eulerian yolu bulan algoritma (Hierholzer Algoritması).
     * @returns {string[]} - Eulerian yol veya hata
     */
    static findEulerianPath(g) {
        if (!this.hasEulerianPath(g)) {
            throw new Error('The graph does not have an Eulerian path.');
        }

        const edges = [...g.edges()];
        const stack = [], path = [];
        const adj = {};

        // Komşuluk listesini oluştur
        edges.forEach(({ v, w }) => {
            if (!adj[v]) adj[v] = [];
            adj[v].push(w);
        });

        let curr = edges[0].v;
        stack.push(curr);

        while (stack.length > 0) {
            if (adj[curr] && adj[curr].length > 0) {
                stack.push(curr);
                curr = adj[curr].pop();
            } else {
                path.push(curr);
                curr = stack.pop();
            }
        }

        return path.reverse();
    }

    /**
     * Hamiltonian yolu bulan algoritma.
     * @returns {string[] | null} - Hamiltonian yolu veya null
     */
    static findHamiltonianPath(g) {
        const nodes = g.nodes();

        for (const start of nodes) {
            const path = [start];
            if (this.dfs(start, new Set([start]), path, g)) {
                return path;
            }
        }

        return null;
    }

    /**
     * Hamiltonian yol için DFS algoritması (backtracking ile).
     * @returns {boolean}
     */
    static dfs(node, visited, path, g) {
        if (visited.size === g.nodeCount()) return true;

        for (const neighbor of g.successors(node) || []) {
            if (!visited.has(neighbor)) {
                visited.add(neighbor);
                path.push(neighbor);

                if (this.dfs(neighbor, visited, path, g)) return true;

                visited.delete(neighbor);
                path.pop();
            }
        }

        return false;
    }

    /**
     * Eulerian veya Hamiltonian yolu döndüren metod.
     * @param {"eulerian" | "hamiltonian"} type - Bulunacak yol türü
     * @returns {string[] | null} - Bulunan yol veya null
     */
    getPath(type) {
        if (type === "eulerian") {
            return GL.findEulerianPath(this.graph);
        } else if (type === "hamiltonian") {
            return GL.findHamiltonianPath(this.graph);
        }
        return null;
    }
}

// Örnek Kullanım:
const nodes = ["A", "B", "C", "D"];
const edges = [{ from: "A", to: "B" }, { from: "B", to: "C" }, { from: "C", to: "D" }, { from: "D", to: "A" }];

const graph = new GL(nodes, edges);

console.log("Eulerian Path:", graph.getPath("eulerian"));
console.log("Hamiltonian Path:", graph.getPath("hamiltonian"));

Bir sorun ile karsilasirsaniz bana sormaktan cekinmeyin.